bayesian-networks
Bayesian Networks
This project was meant to be an example to be given during my quantum machine learning mini-course. However, due to the amount of time I was given, I decided to remove these example about Bayesian Networks and focus specially on Quantum Convolutional Neural Networks.
Although it was a small snippet of code, I think that it deserved some attention. So, here I am, check out what I did.
How to Run
All this code was done using Python and PennyLane, so you may need to have Python3.10 installed as well as all the dependencies required for this project. I recommend you to use mamba/conda-lock, but feel free to use whatever you want.
#mamba setup
mamba env create -f environment.yml
#conda-lock setup
conda-lock install -n bays conda-lock.yml
#pip setup
pip install -r requirements.txt
With all configured, you can run:
jupyter lab bayesian-network.ipynb
Explanation
Is pretty common to see out there, some explanations about Bayesian Theorem using a disease and a test that can give either the correct or the wrong answer (like false positives and negatives). For this case, it won’t be different.
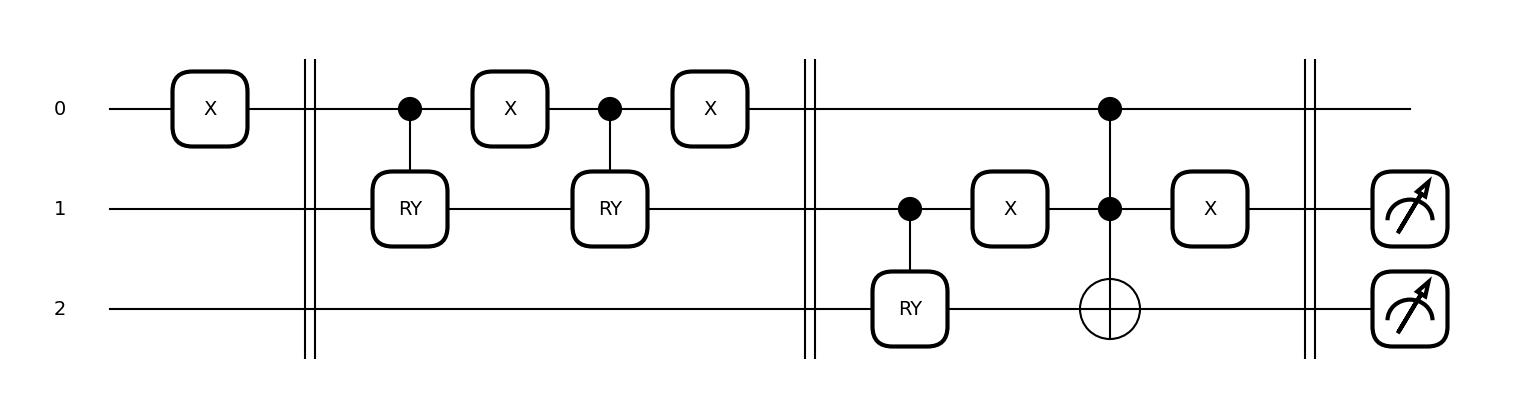
A similar probability case was mapped into a quantum circuit with all probabilities embedded as rotations. This way, each qubit has some probability to be in a certain classical state based on the odds pre-modeled.
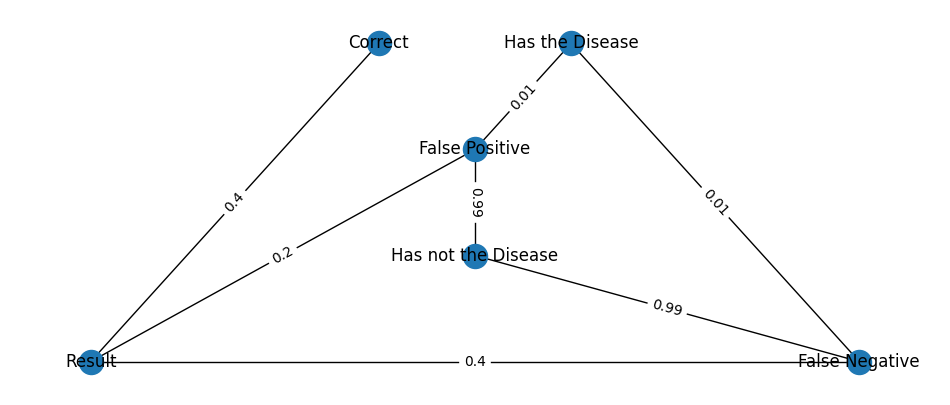
This kind of network can be seen as a graph, where node is a state and every weight on the edges represents the probability to go to a certain state (much like a automaton).
| qubit | Meaning |
|---|---|
| 0 | positive(1) negative(0) |
| 1 | false psotive/negative |
| 2 | chance of having the disease |
| odds | to |
|---|---|
| 0.2 | false positive |
| 0.4 | false negative |
| 0.01 | have the disease given a false positive/negative |
Following this structure, it’s very straightforward to create the circuit.

In this case, the first qubit will act as an input, telling what was the test result (positive/negative), then the probability chain will be in charge to compute the probabilities based on the previous state.
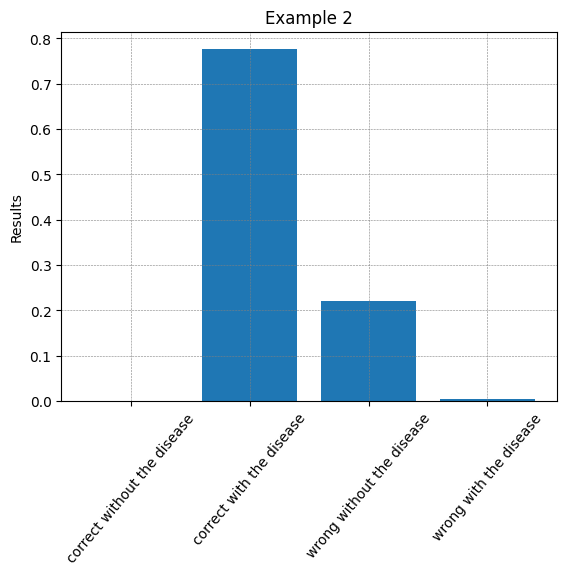
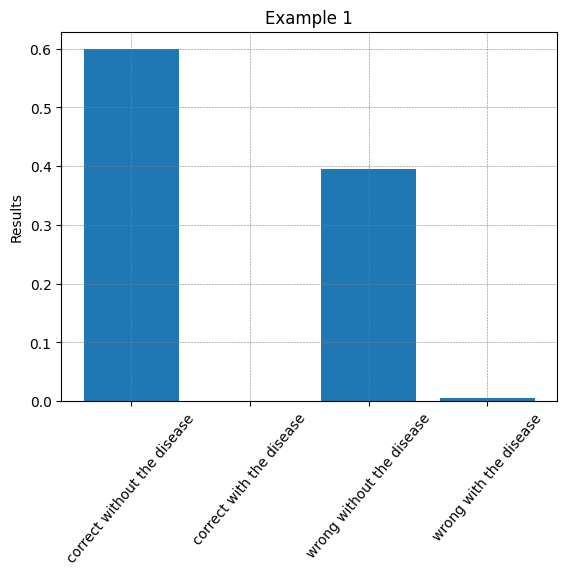
After measuring the last two qubits, we have the following distribution:
The same can be experienced when the result value is 1.