optimization-path
Path Optimization Algorithms
Sometime ago, while I was coming back from college, I starting thinking about the path my bus takes to pass through each university. I was wondering, does it take the best path possible?
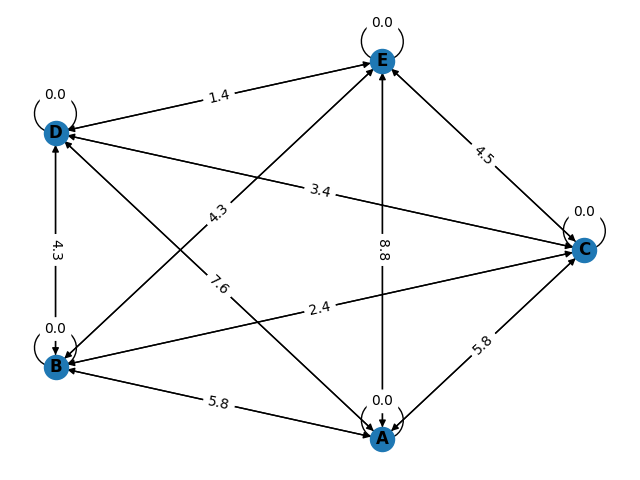
The relations between each university can be seen as graph. Each node corresponds to a single university and each edge distance between them.
My Bus, takes the path A -> B -> C -> D -> E, but is it the best one?
Well, to answer that I implement 5 algorithms for path optimization to check it.
Classical
The first part of this project consists in 4 classical algorithms for this kind of problem, which are:
- greedy algorithm
- brute force
- Dijkstra
- Kruskal
They were implemented in R and can be found at: classical.R.
Run Classical Version
To run the classical version, you must have installed:
if you’re using whatever distro based on Debian, there’s a setup script that install all the dependencies required to run these algorithms. To do that, run:
chmod +x setup-debian.sh
./setup-debian.sh
Note: RStudio will also be installed in this process
With all dependencies downloaded, run on your terminal:
cd ./classical
make install
make run
# or
cd ./classical
sudo Rscript ./installation.R
Rscript classical.R
as result, you must see something like this:
[1] "************************"
[1] "Running Greedy algorithm"
[1] "************************"
[1] "Path: "
[1] "A, B, C, D, E"
[1] "Total length: 13.1"
[1] "************************"
[1] "Running Brute Force algorithm"
[1] "************************"
[1] "Path: "
[1] "A, B, C, D, E"
[1] "Total length: 13.1"
[1] "************************"
[1] "Running Dijkstra algorithm"
[1] "************************"
[1] "Path: "
[1] "A, B, C, D, E"
[1] "Total length: 13.1"
[1] "************************"
[1] "Running Kruskal algorithm"
[1] "************************"
[1] "Path: "
[1] "A, B, C, D, E"
[1] "Total length: 13.1"
Quantum Version
Finally, the problem was converted to quantum in format of a QUBO problem. This way, it was possible to minimize the path based on the binary relation between encoded variables.
To implement this version I used Dimod a python API from D-Wave to interact with samplers and develop QUBO applications.
The Formula
To encode this problem, first we have to clean the set of all edges from the graph, in this case we need to ignore those that either $W(e) = 0.0$ or its target node is the initial node $A$. The set of valid edges will be named as $E = {AB, AC, AD, …, ED}$.
The first term of our QUBO implementation is: $\sum_{i=0}^{n}{E_{i}x_{i}}$, being $n$ the number of elements in $E$.
For this specific setup, 3 constraints are required:
- only 4 nodes are going to be visited
- only 1 node is visited at each step
- loops are not created
the specific formulation for each one is respectively:
$P(\sum_{i=0}^{n}{x_i}-4)^2$
$P(\sum_{step=1}^{n_{steps}}(\sum_{i=0}^{n}{x_i}-1))^2$
$P(\sum_{target}(\sum_{relation_{target}}{x_i}-1))^2$ Where $target$ is the node and $relation$ is a joint of two nodes with the target node being the current $target$ factor in the summation.
Doing that, the final formulation is:
\[\sum_{i=0}^{n}{E_{i}x_{i}} + P(\sum_{i=0}^{n}{x_i}-4)^2 + P(\sum_{step=1}^{n_{steps}}(\sum_{i=0}^{n}{x_i}-1))^2 + P(\sum_{target}(\sum_{relation_{target}}{x_i}-1))^2\]Executing this with Dimod we have as result:
Path: AB BC CD DE
Path size: 13.1
Being the same as the classical version, which is what we expected.
Run Quantum Version
If you want to check it out, open the notebook qubo-version and also take a look at the exported results from the execution results.
To run it you may have:
- python 3.12
- conda/mamba/conda-lock (optional)
Then install the python dependencies:
# using pure conda/mamba
conda env create -f environment.yml
conda activate path-optimization
# using conda-lock
conda-lock install conda-lock.yml -n path-optimization
conda activate path-optimization
# using pip (remember to create a venv before)
pip install -r requirements.txt
Doing so, just type:
jupyter lab qubo-version.ipynb
and start playing with it.
Miscellaneous
There’s also a tiny script to build the graph you saw above. If you want to test it, feel free to check build-graph.py.
Final Thoughts
After finishing this project, it’s possible to conclude that the bus was already taking the optimal path, traveling $13.1 Km$ in total.