qnqueens

Quantum NQueens

Solving NQueens using quantum computing

After becoming obsessed with this problem as I implemented a solution here and here for my AI class at college. I decided to put an end in this story and implement the final version using quantum computing.

At first, I implemented 2 versions one using Qubo and the other QAOA. Even thought the QAOA approach was kinda trick to get good results, I put a lot of effort on that.

During the implementation of this code, I came across this paper, proposing an specific quantum circuit for solving NQueens. I really liked the idea so I decided to create another version by my own.

Using the code

To ease the process of setting up this code, you can use it at:

But you can also run it on your local machine. To do that, first install uv and then run:

uv sync
jupyter lab

Versions

QUBO

The qubo version, which you can find here, was the simplest one to implement.

To do that, I employed the Dwave’s Ocean SDK to generate and sample the Qubo formula.

The formula itself is the following:

\[\sum_{ij}\sum_{a}x_{ij}x_{a} + P(\sum_{ij}x_{ij} - n)^2 = 0\]

Being $ij$ a combination of $row,column$, $a$ a combination of $ij$ for each possible attack at $ij$, $P$ the Lagrange term for penalty and $n$ the board side.

This equation, express that, the combination of each attack should be zero and in total only $n$ queens must appear ($n$ ones).

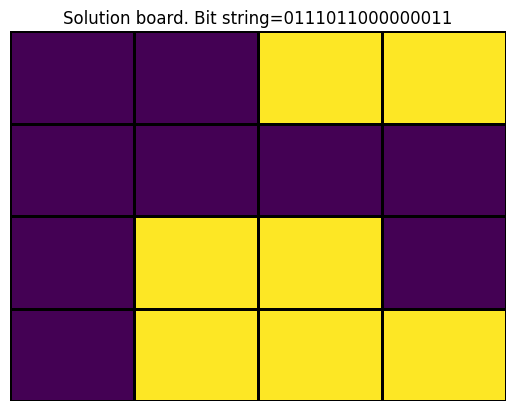
After executing this using two different samplers we got this:

QAOA

Based on the Qubo formulation, we can easily map a binary problem into an ising problem. To do that, we need to manipulate every ising variable to behave as the binary version.

\[x_{i} = {(1-z_{i})\over{2}}\]

So, our qubo becomes:

\[\sum_{ij}\sum_{a}{(1-z_{ij})\over{2}}{(1-z_{a})\over{2}} + P(\sum_{ij}{(1-z_{ij})\over{2}} - n)^2 = 0\]

We could rewrite this as:

\[\sum_{ij}\sum_{a}{1\over{4}}{(1-z_{ij})}{(1-z_{a})} + P(\sum_{ij}{1\over{2}}{(1-z_{ij})} - n)^2 = 0\] \[{1\over{4}}\sum_{ij}\sum_{a}{(1-z_{ij})}{(1-z_{a})} + P({1\over{2}}\sum_{ij}{(1-z_{ij})} - n)^2 = 0\] \[{1\over{4}}\sum_{ij}\sum_{a}{(1 - z_{a} - z_{ij} + z_{ij}z_{a} )} + P({1\over{2}}{|ij|} - n -\sum_{ij}{z_{ij}})^2 = 0\] \[{1\over{4}}{|ij||a|}\sum_{ij}\sum_{a}{(- z_{a} - z_{ij} + z_{ij}z_{a} )} + P(({1\over{2}}{|ij|} - n) -\sum_{ij}{z_{ij}})^2 = 0\]

Being $

ij

$ and $

a

$ the amount of positions and attacks respectively.

After that, we can Embed this as a Hamiltonian inside a QAOA Ansatz, and them minimize its cost using a classical optimizer (like COBYLA).

Once it couldn’t find the solution, I tried a different approach, given the algorithm $10$ tries to explore more parameters.

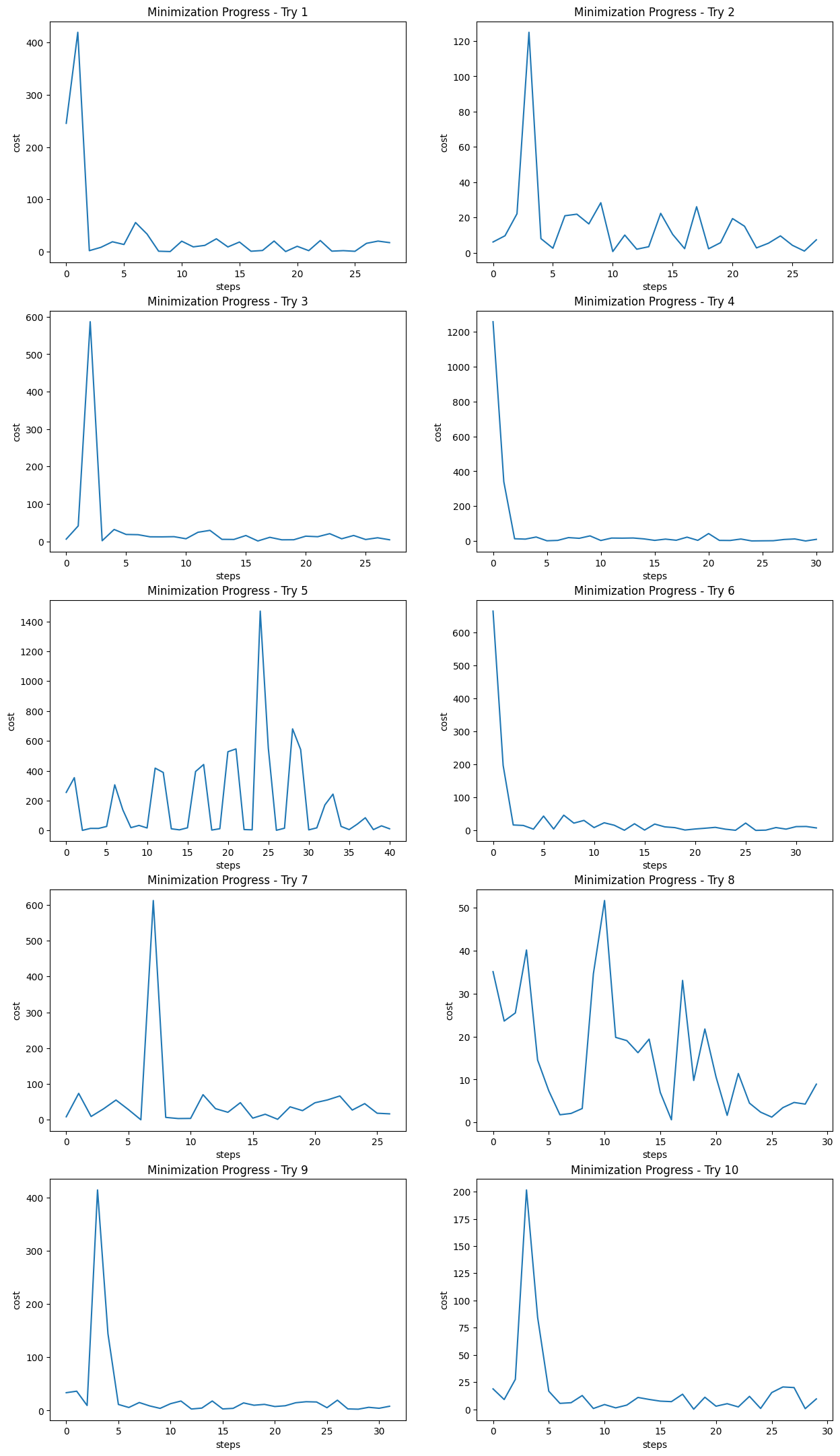
However, it was still stuck in local optima. If you want to help me improve that, feel free to open an issue/PR.

Circuit based

As inspired by arXiv:2312.16312 I decided to create a circuit myself. At first glance, I did a Grover’s algorithm setup to solve this problem. However, during the process, I figured out that using it might be a big overhead, and doing the simple state setup and them checking is better.

In my setup, we have $2N$ qubits, being $N$ the total os cells in the board. The first register (first N qubits) consists of the state based on $W$ states tailored to have both unique rows and columns. After that, we apply a $MCX$ gates checking if each diagonal attack for each position and saving its values to its respective qubit on the second register.

Especial W state

To create this especial $W$ state, we first apply the default $n$ $W$ state, being $n$ the side of the board. Then, for each new block, we check the previous ones, letting empty spaces within the new state. Doing that, at each new block, we reduce the size of the $W$ state until it becomes $1$.

When we reach the $1$ size, we can do create the states ourselves using $MCX$ gates applying it to the last first register block.

Complexity

Even thought the amount of qubits grows linearly as the amount of cells grows $O(N)$, it still very costly to run, since the smallest board ($4x4$) raises a circuit $32$ qubits long.

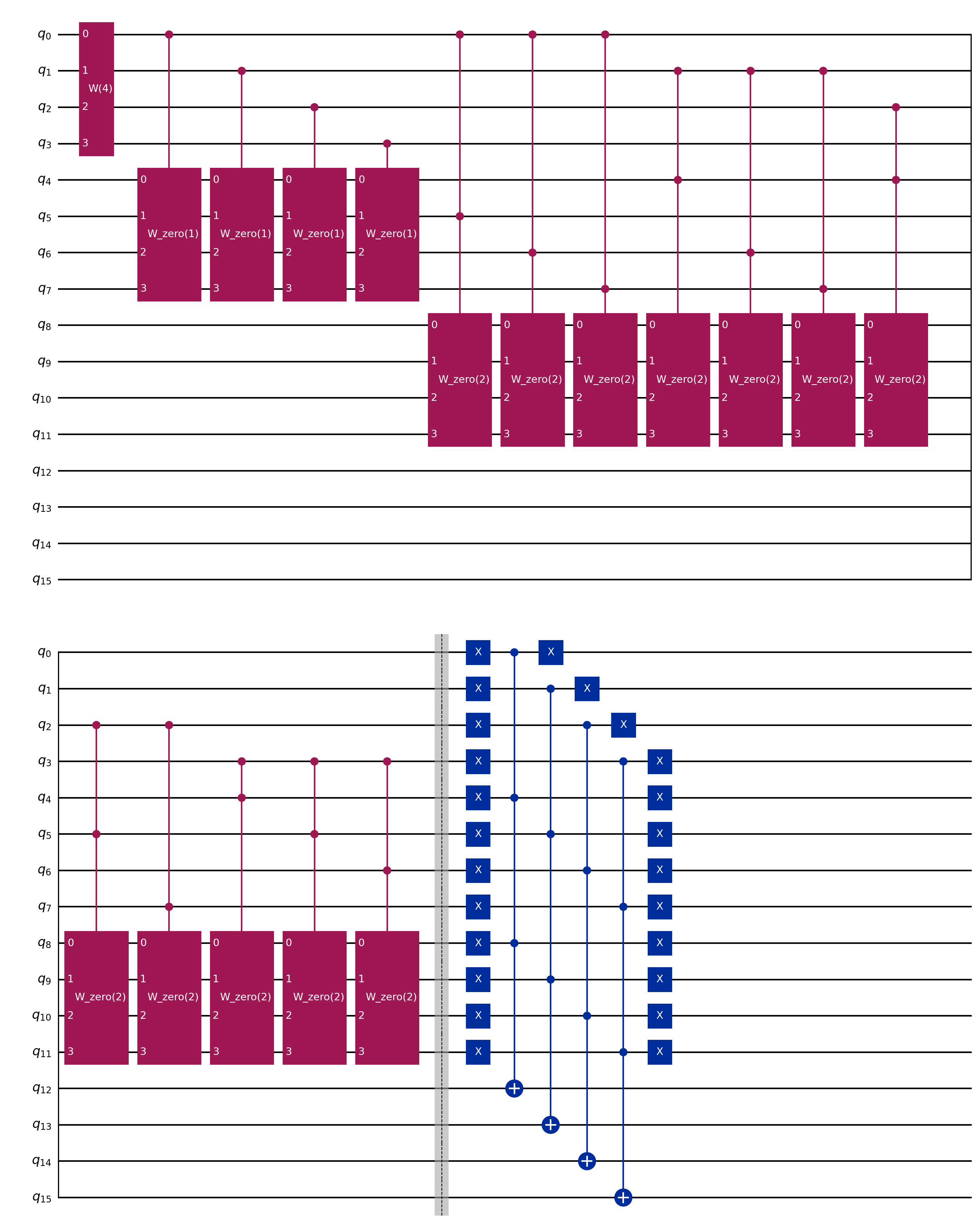
Due to that, it wasn’t possible to test on my humble intel i5. So for Testing the $4x4$ board, I used the ibm_torino backend. However, this amount of qubits was enough to raise a tone of errors and by the end it wasn’t possible to reliably get the final answer.